Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 24

10.24 Determine o momento de inércia da área em relação ao eixo x .

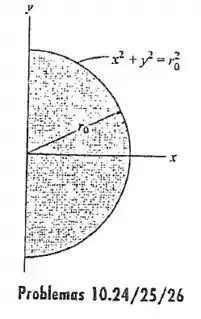
Passo 1

A fórmula do momento de inércia em relação ao eixo x é

I x = ∫ A y 2 d A

Nós precisamos escolher um elemento infinitesimal de área que seja paralelo ao eixo x :

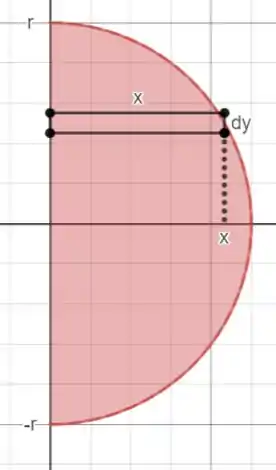
O elemento infinitesimal de área vai ser igual a

d A = x d y

Isolando x na função dada:

x 2 + y 2 = r 0 2

x 2 = r 0 2 - y 2

x = r 0 2 - y 2

Então

d A = r 0 2 - y 2 d y

E os limites de integraçãoo vão ir de - r 0 até r 0 .

Passo 2

Agora é só reolver a integral

I x = ∫ A y 2 d A

I x = ∫ - r 0 r 0 y 2 r 0 2 - y 2 d y

Vamos usar a técnica de substituição

y = r 0 sen ⁡ u

Então

d y = r 0 cos ⁡ u d u

Os limites de integração vão ficar dessa forma:

Quando y → - r 0

- r 0 = r 0 sen ⁡ u

sen ⁡ u = - 1

u = - π 2

E quando y → r 0

r 0 = r 0 sen ⁡ u

sen ⁡ u = 1

u = π 2

A equação fica

I x = ∫ - π / 2 π / 2 ( r 0 sen ⁡ u ) 2 r 0 2 - ( r 0 sen ⁡ u ) 2 ⋅ r 0 cos ⁡ u d u

I x = ∫ - π / 2 π / 2 r 0 2 sen 2 ⁡ u ⋅ r 0 2 ( 1 - sen 2 ⁡ u ) ⋅ r 0 cos ⁡ u d u

I x = ∫ - π / 2 π / 2 r 0 2 sen 2 ⁡ u ⋅ r 0 1 - sen 2 ⁡ u ⋅ r 0 cos ⁡ u d u

I x = ∫ - π / 2 π / 2 r 0 4 sen 2 ⁡ u ⋅ 1 - sen 2 ⁡ u ⋅ cos ⁡ u d u

Pelas relações trigonométricas, nós sabemos que

sen 2 ⁡ u + cos 2 ⁡ u = 1

cos 2 ⁡ u = 1 - sen 2 ⁡ u

cos ⁡ u = 1 - sen 2 ⁡ u

Podemos substituir o cos ⁡ u na integral.

I x = ∫ - π / 2 π / 2 r 0 4 sen 2 ⁡ u ⋅ cos ⁡ u ⋅ cos ⁡ u d u

I x = ∫ - π / 2 π / 2 r 0 4 sen 2 ⁡ u ⋅ cos 2 ⁡ u d u

Aqui vamos ter que lembrar de umas bruxarias da trigonometria

sen ⁡ 2 a = 2 sen ⁡ a ⋅ cos ⁡ a

sen ⁡ a ⋅ cos ⁡ a = sen ⁡ 2 a 2

Se a gente elevar ao quadrado, os dois lados dessa equação:

sen 2 ⁡ a ⋅ cos 2 ⁡ a = sen 2 ⁡ 2 a 4

Então podemos reescrever a integral, como:

I x = ∫ - π / 2 π / 2 r 0 4 sen 2 ⁡ ( 2 u ) 4 d u

Vamos tirar as constantes para fora da integral

I x = r 0 4 4 ∫ - π / 2 π / 2 sen 2 ⁡ ( 2 u ) d u

Mais uma coisinha da trigonometria:

sen 2 ⁡ a = 1 - cos ⁡ 2 a 2

Então

sen 2 ⁡ ( 2 u ) = 1 - cos ⁡ 4 u 2

Substituindo na integral

I x = r 0 4 4 ∫ - π / 2 π / 2 1 - cos ⁡ 4 u 2 d u

Tirando, novamente, a constante para fora da integral

I x = r 0 4 8 ∫ - π / 2 π / 2 1 - cos ⁡ 4 u d u

I x = r 0 4 8 u - sin ⁡ 4 u 4 - π 2 π / 2

I x = r 0 4 8 π 2 - sin ⁡ 4 π 2 4 - - π 2 - sin ⁡ 4 - π 2 4

I x = r 0 4 8 π 2 - 0 - - π 2 - 0

I x = r 0 4 8 π

Resposta

I x = r 0 4 8 π

Ver Outros Exercícios desse livro