67- O carrinho de plataforma sustenta três cargas mostradas na figura. Determine as reações normais em cada uma das três rodas.
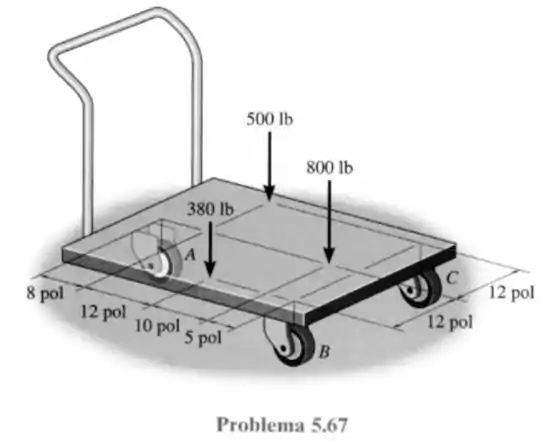
Passo 1
Vamos criar os eixos coordenados na figura para que possamos calcular as forças.
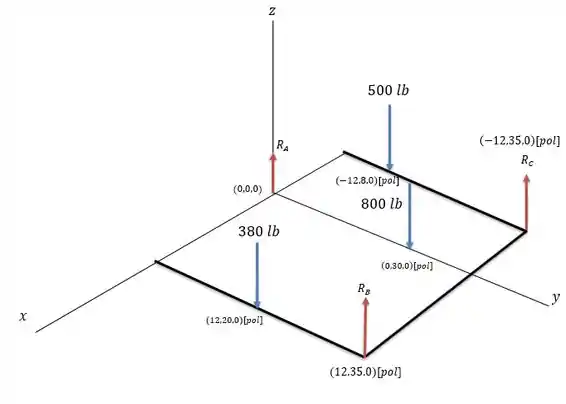
Assumindo que a reação na roda vale , na roda vale e na roda vale .
Passo 2
Fazendo a somatória das forças no eixo temos:
Agora fazendo a somatória dos momentos no eixo temos (adotando sentido anti-horário negativo)
Passo 3
Agora fazendo a somatória dos momentos no eixo (adotando sentido anti-horário negativo)
Essa equação com a do passo anterior nos dá:
Passo 4
Substituindo esses resultados na somatória das forças verticais nós teremos: