Os ângulos entre o vetor e os eixos coordenados são e . Os cossenos desses ângulos são conhecidos como cossenos de direção. Avalie os cossenos de direção em termos dos componentes de F. Mostre que
Passo 1
Faaaala galera, beleza? Vamos lá resolver mais uma questão juntos?!
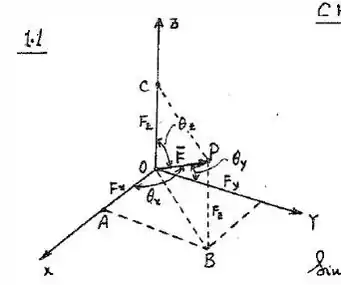
Segue-se então que
similarmente
Passo 2
Pelo teorema de Pitágoras
E foi isso, vamos pra próxima 😊