Aproxime a forma do Lago Superior por um círculo de raio em uma latitude de . Suponha a água em repouso em relação à Terra e determine a profundidade da depressão no centro em relação às margens por causa da força centrífuga.
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Nessa questão temos que a superfície da água não vai ser exatamente tangente a superfície da Terra por esse movimento de rotação dela. Então vamos calcular quanto é essa profundidade que temos.
Passo 2
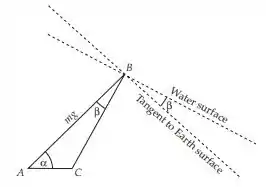
Usando o teorema dos cossenos para encontrar o lado BC desse triângulo da figura, temos
Onde AC é a força centrifuga com com e o raio da Terra .
O ângulo que a superfície é desviada da direção tangencial da superfície da Terra pode ser achado pela lei dos senos. Assim,
Substituindo os valores e fazendo as contas, temos
Dessa forma, a altura que o lago cai pode ser calculado por onde que é o raio do lago. Substituindo o valor achado de encontramos
Resposta
A altura é de .
Mais um problema feito. Bora pra mais um?