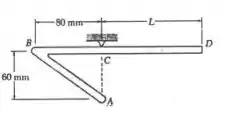
Um arame homogêneo ABCD é dobrado, como se vê na figura. Em C o fio é preso por uma articulação. Determine o comprimento L para que a parte BCD fique em posição horizontal.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
Vamos iniciar fazendo o noss D.C.L do fio homogêneo ABCD dividindo-o em três segmentos
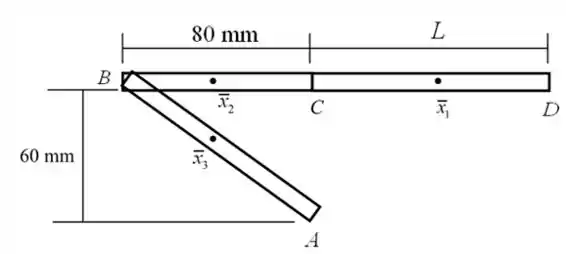
Passo 2
Como o fio é homogêneo, o centro de gravidade do fio coincidirá como o centroide da linha correspondente.
Calcularemos o comprimento do fio para a parte AB.
Calculando o comprimento do fio para a porção CD
Onde
é o centroide de segmento 1.
é o comprimento do segmento 1.
é o centroide de segmento 2.
é o comprimento do segmento 2.
é o centroide de segmento 3.
é o comprimento do segmento 3.
Resposta
Portanto, o comprimento do fio CD é de .