Um arco fino de raio R e massa M oscila em seu próprio plano pendurado por um único ponto fixo. Ligada ao aro está uma pequena massa M restringida ao movimento (sem atrito) ao longo do aro. Considere apenas pequenas oscilações e mostre que as autofrequências são:
Encontre os dois conjuntos de condições iniciais que permitem ao sistema oscilar em seus modos normais. Descreva a situação física para cada modo.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações acopladas.
O esquema do problema apresentado:
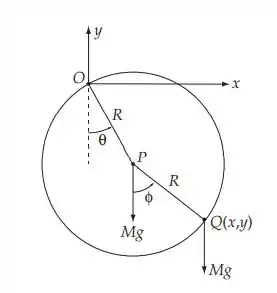
Seja O o ponto fixo no aro e a origem do sistema de coordenadas. P é o centro de massa do aro e Q(x,y) é a posição da massa M. As coordenadas de Q são:
A inércia rotacional do aro através de O é:
A energia potencial do sistema é:
Como θ e φ são ângulos pequenos, podemos usar . Então, descartando o termo constante em U, temos:
A energia cinética do sistema é:
Onde usamos novamente as aproximações de pequeno ângulo para θ e φ. Desta forma:
Usando Eqs. (12.34):
Identificamos os elementos de {m} e {A}:
Que nos dá o determinante:
Do qual:
Resolvendo para as frequências próprias, encontramos:
Para obter os modos normais, devemos resolver:
Para k = r = 1, isso se torna:
Ou:
Para k = 1, r = 2, o resultado é:
Assim as equações:
Podem ser reescritas como:
Resolvendo para η1, η2:
Sendo que:
Este é o modo antissimétrico em que o CM do aro e a massa estão em lados opostos da vertical através do ponto de pivô.
E:
Este é o modo simétrico em que o ponto de pivô, o CM do aro e a massa sempre estão em uma linha reta.
Resposta
Ver passo a passo.