Um aro circular é suspenso em um plano horizontal por três fios, cada um com comprimento , que são conectados simetricamente ao aro e aos pontos fixos dispostos em um plano sobre o aro. Em equilíbrio, cada fio é vertical. Demonstre que a frequência de oscilações rotacionais sobre o vertical através do centro do aro é a mesma que para um pêndulo simples de comprimento .
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Primeiro vamos entender o que está rolando nesse exercício. Temos um plano e um aro que está ligado a esse plano por três fios, simétricos e estão fixos no plano. O aro que se move e vai girar com pequenas oscilações. Segue o desenho que vai ajudar.
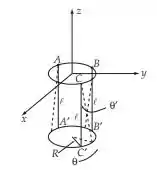
Os pontos , e são os pontos fixos no plano e os pontos , e são os pontos no aro e que vão girar. Primeiro precisamos achar a energia cinética e potencial como sempre nesse tipo de exercício. Como os eixos e são fixos, vamos usar as coordenadas e , já que é nessas coordenadas que o movimento vai acontecer.
Passo 2
Para a energia cinética temos a parte rotacional e a parte translacional, então vai ficar
Como temos um aro, vamos ter
E como vamos ter a energia cinética na forma
O termo é uma derivada de em relação a e pode ser colocado como uma derivada de através pela regra da cadeia, ficando na forma
Substituindo na equação da Energia Cinética, temos
Mas como queremos para pequenas oscilações, o termo da derivada de em relação a será zero, assim a energia cinética fica
Para a energia potencial, temos
Mas olhando o sistema da figura, temos que depende de , e . Vamos entender como.
Olhando apenas pro plano do aro, vamos ter um pequeno ângulo, que vamos aproximar pra um triângulo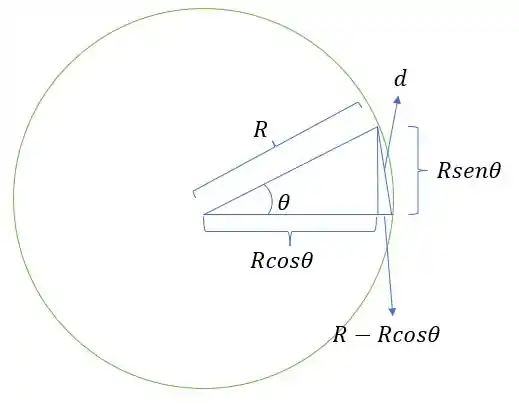
Como vemos na imagem, temos que esse pode ser encontrado aplicando o teorema de Pitágoras, sendo que seus catetos são e .
Agora vendo o triângulo maior, que é formado por , e , já que a distância que ele deslocou quando fez o ângulo foi . Assim, vamos ter
Substituindo o valor de que achamos, ficamos com
Isolando temos
Levando em conta que quando temos , escrevemos
Tendo o , podemos escrever a energia potencial
Como estamos considerando o ângulo pequeno, podemos usar a aproximação . Substituindo na nossa equação da energia potencial, temos
Colocando em evidência na raiz e tirando ele para fora, temos
Como sabemos que é pequeno, essa expressão com também é pequena e assim podemos aplicar a aproximação de Taylor, onde temos
Substituindo na expressão da energia potencial, temos
Passo 3
Tendo as duas energias, é só encontrar a Lagrangiana e as equações de movimento pelas equações de Euler-Lagrange.
Como as equações de Euler-Lagrange são
Temos
Observando essa equação, temos que a frequência de oscilação é a mesma do pêndulo simples, sendo
Resposta
Como no pêndulo simples.
Mais um problema feito. Bora pra mais um?