Um aro de massa m e raio R roda sem deslizar para baixo de um plano inclinado de massa m, que forma um ângulo a com a horizontal. Encontre as equações de Lagrange e as integrais de movimento se o plano puder deslizar sem fricção ao longo de uma superfície horizontal.
Passo 1
Faaaaaala, galera... Tranquileba??
Façamos um esboço da situação dita no enunciado:
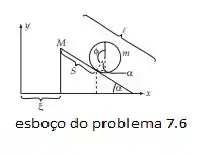
Onde decidimos escolher e como nossas coordenadas generalizadas. Assim as coordenadas x y para o centro do aro são expressos por:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
De onde podemos a energia cinetica, que é:
Usamos que e :
E como dito, o plano também desliza, logo:
Assim, a energia total é:
E a energia potencial é somendo do aro:
E enfim a lagragiana é:
Passo 3
E a matriz de equação de movimento para as coordenadas e
Assim: