Um balde de água é mantido em giro sobre seu eixo de simetria. Determine a forma da água no balde.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de movimento em um sistema de referência não inercial.
A partir do enunciado temos o esquema do problema:
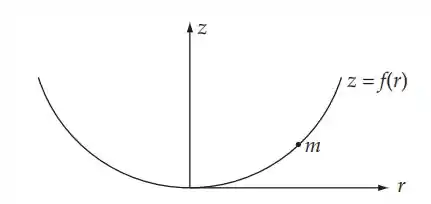
Considere uma pequena massa m na superfície da água. Da Eq. (10,25):
Na estrutura rotativa, a massa está em repouso; portanto: .
A força F consistirá da gravidade e da força devido ao gradiente de pressão, que é normal à superfície em equilíbrio. Desde que:
Agora temos:
Onde Fp é devido ao gradiente de pressão.
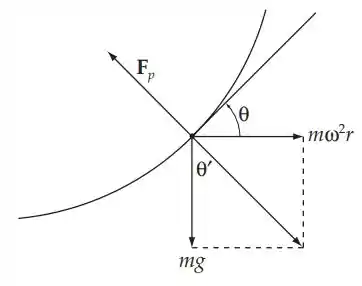
Como , a soma das forças gravitacional e centrífuga também deve ser normal à superfície. Então .
E como:
Temos que:
A forma é um parabolóide circular.
Resposta
Ver passo a passo.