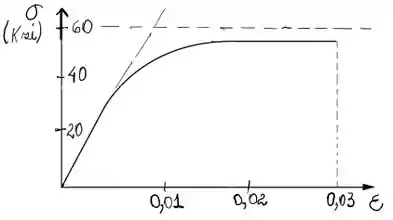
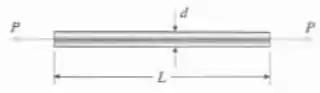
Uma barra circular de comprimento , e diâmetro , está submetida à tração pelas forças (veja a figura). O fio é feito de uma liga de cobre tendo a seguinte relação hiperbólica de tensão-deformação:
- Desenhe um diagrama de tensão-deformação para o material. (b) Se o alongamento do fio está limitado a e a tensão máxima está limitada , qual o valor da carga admissível ?
Passo 1
Bora lá galera!
Dados:
Passo 2
- Diagrama tensão-deformação
- Carga permitida
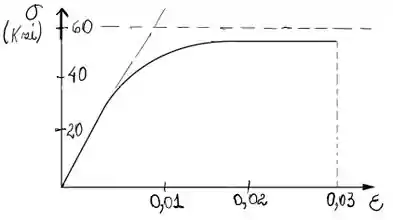
Obs: finge que tá reto rs!!!
![]()
Passo 3
Alongamento máximo
Tensão máxima
Com base no alongamento, temos que:
E com base na tensão, temos que a tensão crítica será , logo:
Essa questão foi, heim... Bora pra próxima?