Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Gere, Mecânica dos Materiais- Ed: 5º - Capítulo 3.3 - Ex. 8

Uma barra circular AB com extremidades fixas contra a rotação tem um furo que se estende até metade de seu comprimento (veja a figura). O diâmetro externo da barra é d 2 = 100   m m e o diâmetro do furo é d 1 = 80   m m . O comprimento total da barra é L = 1.250   m m .

A qual distância x da extremidade esquerda da barra um torque T 0 deve ser aplicado de forma que os torques de reação nos suportes sejam iguais?

Passo 1

Fala galerinha, bora lá?

Vamos iniciar desenhando o nosso D.C.L

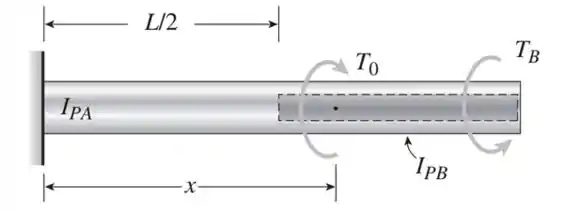
Passo 2

Considerando a condição dada, os torques nas extremidades A e B devem ser iguais.

T A = T B

Considerando o equilíbrio de torque ao longo do eixo do eixo

T A + T B = T 0

Substituindo T A   p o r   T B

T A + T A = T 0

T A = T B = T 0 2

Passo 3

Considerando o ângulo de torção na extremidade B usando a equação 3-48 do livro.

ϕ B = T B l 2 G I P B + T B l 2 G I P A - T 0 x - l 2 G I P B - T 0 l 2 G I P A

Substituindo T A   e   T B

ϕ B = T 0 2 l 2 G I P B + T 0 2 l 2 G I P A - T 0 x - l 2 G I P B - T 0 l 2 G I P A

ϕ B = T 0 G L 4 I P B + L 4 I P A - x I P B + L 2 I P B - L 2 I P A

Aplicando a compatibilidade

ϕ B = T 0 G L 4 I P B + L 4 I P A - x I P B + L 2 I P B - L 2 I P A = 0

Resolvendo para x

x = ( 3 I P A - I P B ) L 4 I P A

Substituindo em I P A   e   I P B

x = 3 π 32 d 2 4 - π 32 d 2 4 - d 1 4 L 4 π 32 d 2 4

x = 2 d 2 4 + d 1 4 L 4 ( d 2 4 )

Passo 4

Substituindo os valores numéricos

x = 2 d 2 4 + d 1 4 L 4 ( d 2 4 )

x = 2 × 100   m m   4 + 80   m m 4 × 1.250   m m 4 × 100   m m 4

x = 753   m m

Resposta

Portanto, o torque T 0 deve ser aplicado a uma distancia de 753 mm da extremidade a esquerda da barra para que o torque reativo no apoio seja igual.