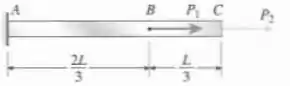
Uma barra prismática de comprimento e área de seção transversal está carregada pelas forças e (veja a figura). A barra é construída de liga de alumínio tendo uma curva de tensão-deformação descrita pela equação de Ramberg-Osgood:
em que tem unidades de megapascals.
- Calcule o deslocamento da extremidade da barra quando a carga age sozinha.
- Calcule o deslocamento quando a carga age sozinha.
- Calcule o deslocamento quando ambas as cargas agem simultaneamente.
Passo 1
Bora lá galera!
Nesse caso, a barra está carregada axialmente.
Dados:
Equação de Ramberg-Osgood:
Passo 2
- Calculando o deslocamento quando a carga age sozinha.
AB
- Calculando o deslocamento quando a carga age sozinha.
- Calculando o deslocamento quando ambas as cargas agem simultaneamente.
Com isso, o deslocamento será:
Passo 3
ABC
Com isso, o deslocamento será:
Passo 4
AB
E o deslocamento será:
BC
E o deslocamento será:
Com isso, o deslocamento da barra quando ambas as cargas agem simultaneamente é:
Essa questão foi, heim... Bora pra próxima?