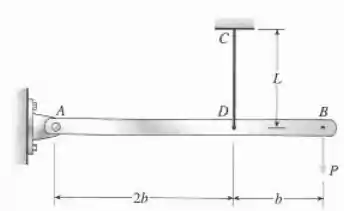
Uma barra rígida , presa por um pino na extremidade , é sustentada por um fio e carregada por uma força na extremidade (veja a figura). O fio é feito de aço de alta resistência tendo módulo de elasticidade e tensão de escoamento . O comprimento do fio é e seu diâmetro é . O diagrama de tensão-deformação para o aço está definido pela lei da potência modificada, da seguinte maneira:
- Assumindo , calcule o deslocamento na extremidade da barra devido à carga . Tome valores para de até em incrementos de .
- Trace um diagrama de carga-deslocamento mostrado .
Passo 1
Bora lá galera!
Dados:
Para o diagrama da tensão-deformação, temos que:
Eq. (1)
Eq. (2)
Deslocamento no final da barraEq. (3)
E para as deformações, das Equações 1 e 2 podemos obter as seguintes expressões:
Pela Eq. (1): Eq. (4) para
Pela Eq. (2): Eq. (5) para
Força axial no fio: Eq. (6)
Passo 2
- Com isso my friends, aplicamos essas equações com uma carga variando de até em incrementos de , logo:
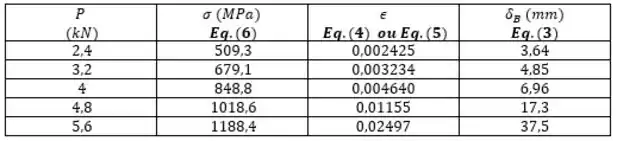
E quando a tensão é , temos que:
Passo 3
Agora, devemos desenhar o diagrama de carga-deslocamento, logo:
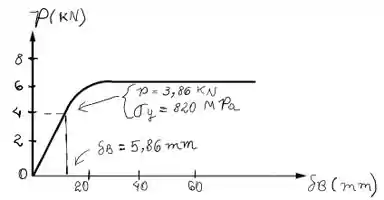
Obs: Finge que tá bonito! Rsrs
Essa questão foi, heim... Bora pra próxima?
Resposta
Ei, a resposta está no passo a passo :)