Um bloco de 150 kg pende de uma pequena polia que pode rolar sobre o cabo ACB. A polia e sua carga são mantidas na posição ilustrada na figura por um segundo cabo DE, paralelo ao trecho CB do cabo. Determine: (a) a tração no cabo ACB e (b) a tração no cabo DE. Despreze o raio da polia e a massa dos cabos e da roldana.
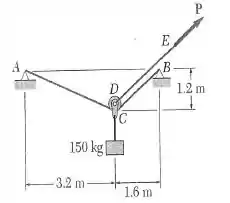
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Já vamos começar a analisar o sistema de forças na polia:
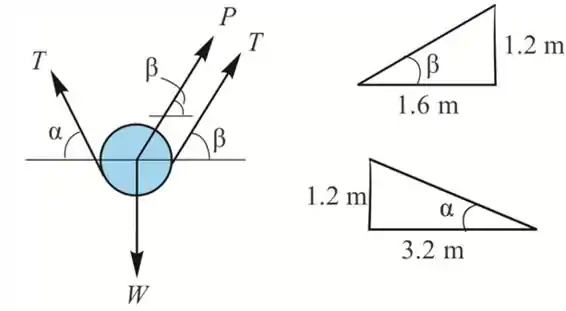
Passo 2
Agora sabemos que o peso do bloco é
Pela figura
Passo 3
- Das equações de equilíbrio ao longo do eixo de x
- Da equação (1)
Passo 4
Das equações de equilíbrio ao longo do eixo y
Portanto, a tensão no cabo ACB é de
Passo 5
Portanto, a tensão no cabo DE é .
Resposta
- Portanto, a tensão no cabo ACB é de
- Portanto, a tensão no cabo DE é .