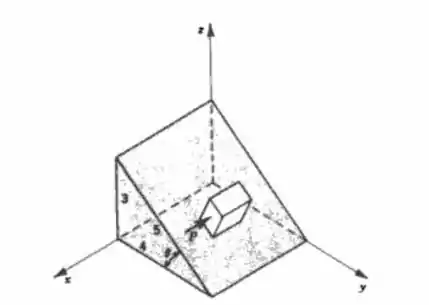
Um bloco de peso W repousa sobre um plano inclinado que faz um ângulo como mostrado. Uma força P, paralela ao eixo x, é aplicada ao bloco e aumentada gradualmente a partir de zero: quando P atinge o valor 0,4W, o bloco começa a deslizar. Qual é o coeficiente de atrito entre o bloco e o plano inclinado?
Passo 1
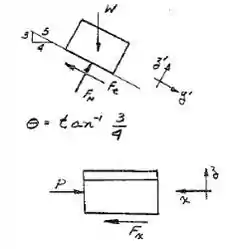
Passo 2
Quando o bloco começa a se mover, P = 0,4 W e a magnitude da força de atrito da equação para a magnitude da soma vetorial de Fe e Fx