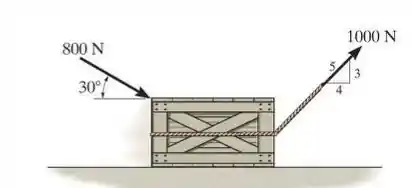
O caixote, que tem massa de 100 kg, está sujeito à ação das duas forças. Se ele está originalmente em repouso, determine a distância que ele desliza para atingir uma velocidade de 6 m/s. O coeficiente de atrito cinético entre a caixa e a superfície .
Passo 1
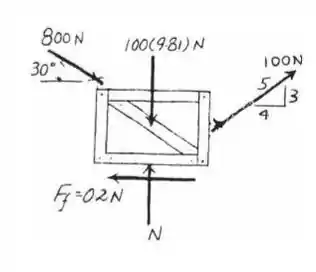
Equações de Movimento: Como o caixote desliza, a força de atrito desenvolvida entre o caixote e sua superfície de contato é. Aplicando a Eq. 13-7, temos
Passo 2
Princípio do Trabalho e da Energia: As componentes horizontais da força 800N e 1000N que atuam na direção do deslocamento realizam trabalho positivo, enquanto a força de atrito realiza trabalho negativo desde atua na direção oposta à do deslocamento. A reação normal N, a componente vertical da força de 800N e 1000N e o peso da caixa não se deslocam, portanto não realizam trabalho. Como o caixote está originalmente em repouso,. Aplicando a Eq. 14-7, temos