Calcule a altura ideal da borda de uma mesa de bilhar. Sobre qual base o cálculo é proposto?
Passo 1
Muitos truques de bilhar são realizados batendo a bola em diferentes alturas e em diferentes
ângulos para transmitir movimento de deslizamento e rotação. Para a mesa não introduzir efeitos espúrios, a borda deve estar a uma altura tal que a bola seja “rebatida” numa colisão.
Considere o caso em que a bola incide normalmente na borda, como no diagrama.
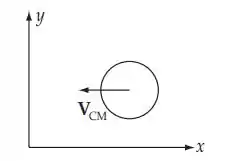
Nós temos as seguintes relações:

Passo 2
Então, temos que:
Assim:
De onde:
Passo 3
Assumindo que a bola rola sem escorregar antes do contato com a borda, então , e obtemos o mesmo resultado de antes:
Passo 4
Assim:
Onde:
Ou:
Resposta
Portanto a altura da borda deve ser de acima do centro da bola.