Calcule os momentos de inércia para um cone homogêneo de massa M cuja altura é h e cuja base tem um raio, R. Escolha o eixo ao longo do eixo de simetria do cone. Escolha a origem do vértice do cone e calcule os elementos do tensor de inércia. A seguir, faça uma transformada de modo que o centro de massa do cone se torne a origem e determine os momentos de inércia principais.
Passo 1
O cone da questão está representado na figura abaixo:
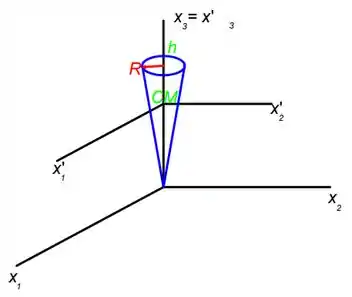
Passo 2
Nessa primeira parte da questão vamos calcular os elementos do tensor de inércia com a origem no vértice do cone, dessa forma vamos olhar para os eixos .
Pela figura é possível perceber que para . Dessa forma os elementos diagonais se tornam os principais momentos , que nós vamos calcular agora.
O cálculo pode ser simplificado fazendo uma observação na figura, pois nela vemos uma simetria entre os planos notados como 1 e 2, assim . Então:
Que em coordenadas cilíndricas, pode ser escrito como:
Onde:
Passo 3
Resolvendo a integral e substituindo por , encontramos:
Passo 4
E é dado por:
Passo 5
De onde temos que:
E essa é a resposta da primeira parte.
Passo 6
Em seguida a questão pede que calculemos os momentos de inércia principais considerando o centro de massa do cone como a origem. Para isso vamos analisar a figura o Passo 1 em relação aos eixos
Passo 7
Devido a simetria do cone, o centro de massa se encontra sobre o eixo . Assim as coordenadas do centro de massa são (), onde:
Passo 8
Usando a forma geral do Teorema do eixo paralelo de Steiner:
Passo 9
Para esse caso, e , então:
E essa é a reposta da segunda parte da questão.
Resposta
Ei, a resposta está no passo a passo :)