Calcule a seção transversal diferencial e a seção transversal total , do espalhamento elástico de uma partícula a partir de uma esfera impenetrável; o potencial é expresso por:
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
A mudança no ângulo para uma partícula de massa µ movendo-se em um campo de força central é dado pela Equação 9.121 (página 324). Daí temos que:
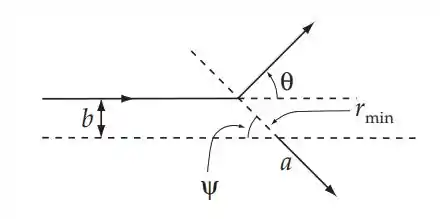
Na dispersão de uma esfera impenetrável, rmin é o raio dessa esfera. Além disso, podemos ver na figura que θ = π − 2ψ.
Para r > rmin, U = 0. Daí:
Substituindo:
Obtemos:
Esta integral pode ser resolvida usando a Eq. (E.10b), Apêndice E:
Desta forma:
Portanto, podemos encontrar a relação entre θ e b substituindo (θ = π − 2ψ) na equação acima, obtendo:
Agora, a seção transversal diferencial é dada pela Eq. (9.120):
A seção transversal total é dada por:
Resposta
Ver passo a passo.