Um canhão instalado em um forte com visão do mar dispara um projétil de massa M em um ângulo de elevação θ e velocidade na boca do canhão v0. No ponto mais alto, o projétil explode em dois fragmentos (massas m1 + m2 = M), com energia adicional E, deslocando-se na direção horizontal original. Determine a distância que separa os dois fragmentos quando eles tocam o mar. Para simplificar, suponha que o canhão se encontra no nível do mar.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
A partir do enunciado temos o esquema do problema:
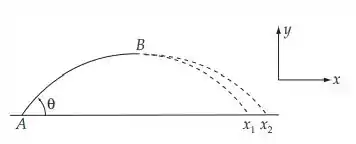
Primeiro, encontramos o tempo necessário para ir de A até B examinando o movimento. A equação para a componente y da velocidade é:
Em B, vy = 0. Então, tB = (v0 sen θ)/g.
A casca explode dando a m1 e m2 velocidades horizontais v1 e v2 (na direção original). Resolvemos para v1 e v2 usando conservação de momento e energia.
Isolando v2 na equação da quantidade de movimento, e substituindo na equação da energia, teremos:
Daí, temos que:
Agora precisamos das posições onde m1 e m2 aterrissam. O tempo para cair no oceano é o mesmo que o tempo que levou para ir de A até B. Chamando o local onde a concha explode x = 0 temos as posições de m1 e m2 no desembarque dadas, respectivamente, por:
Então:
Usando as equações obtidas para v1 e v2, temos que:
Resposta
Ver passo a passo.