O carregamento distribuído atuando sobre uma viga engastada tem uma intensidade dada pela expressão ,em que é a máxima intensidade do carregamento (veja a figura). Derivar a equação da curva de deflexão e então determinar a deflexão na extremidade livre. Use a equação diferencial de quarta ordem da curva de deflexão (a equação do carregamento).
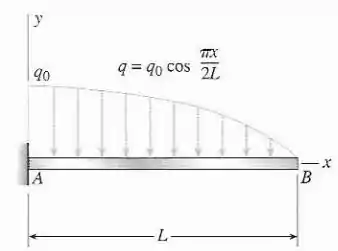
Passo 1
Bora lá galera!
Usando a equação diferencial de quarta ordem, como diz o enunciado:
Eq. (1)
Eq. (2)
Aplicando as velhas e conhecidas condições de contorno e integrando, temos que:
Condição de contorno - 1
Eq. (3)
Condição de contorno - 2
Eq. (4)
Condição de contorno - 3
Eq. (5)
Condição de contorno - 4
Passo 2
Com isso, meus caros amigos, ao aplicarmos todas essas condições na equação 5, temos que:
E, portanto, a deflexão na extremidade livre, será:
Substituindo o por , finalmente temos:
Essa questão foi, heim... Bora pra próxima?
Resposta