O centro de gravidade de um sistema de partículas é o ponto sobre o qual as forças gravitacionais externas não exercem nenhum torque líquido. Para uma força gravitacional uniforme, demonstre que o centro de gravidade é idêntico ao centro de massa para o sistema de partículas.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
O diagrama (um desenho) do que o enunciado pede facilita a visualização do que é necessário para resolver o problema:
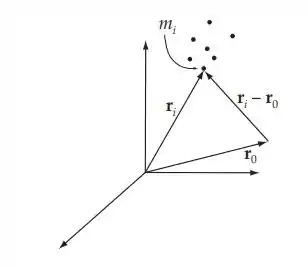
Temos as seguintes definições:
Calculando o torque em torno de r0:
Agora, se o torque total é zero, devemos ter:
Que é a definição do centro de massa. Então:
Ou centro de gravidade = centro de massa.
Resposta
Ver passo a passo.