Uma chapa homogênea de espessura a é colocada sobre um cilindro fixo de raio R cujo eixo é horizontal. Demonstre que a condição de equilíbrio estável da chapa, supondo a ausência de escorregamento, é R > a/2. Qual será a frequência das pequenas oscilações? Desenhe um gráfico da energia potencial U como função do deslocamento angular . Demonstre que existe um mínimo em para R > a/2, mas não para R
Passo 1
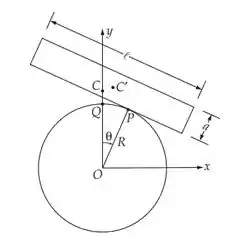
O diagrama mostra a chapa rotacionando a um ângulo a partir de sua posição de equilíbrio. No equilíbrio o ponto de contato é e após a rotação o ponto de contato é . No equilíbrio o
a posição do centro de massa da chapa é e após a rotação a posição é .
Como estamos considerando apenas pequenas alterações, iniciando em , podemos escrever:
Portanto as coordenadas de serão:
Passo 2
Então:
Consequentemente:
De onde podemos dizer:
Passo 3
A energia cinética é:
Onde é o momento de inércia da chapa em relação a um eixo que passa pelo centro de
massa e paralela ao eixo :
Portanto:
Onde:
Já a energia potencial é:
Substituindo o valor de encontrado no Passo 1, temos:
Passo 4
A equação de Lagrange para é:
Então, agora:
Combinando as equações, temos:
Passo 5
Para o caso de pequenas oscilações, e , então a equação final do Passo 4 pode ser reduzida para:
O sistema é estável para oscilações próximas de , apenas se:
E essa condição só é satisfeita se , então
Então a frequência, escrito de uma forma simplificada, é:
Passo 6
De acordo com o Passo 3 a energia potencial tem as seguintes formas para e :
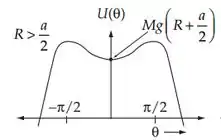
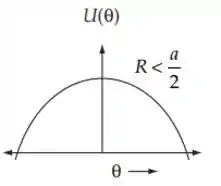
Passo 7
Para verificar que a condição de estabilidade existe apenas para , é preciso verificar com :
Resposta
Ei, a resposta está no passo a passo :)