Classifique cada uma das estruturas dadas como completa parcial ou ineficazmente vinculada. Se completamente vinculada, classifique ainda como determinada ou independente. (Todas as barras podem estar submetidas a tração ou a compressão).
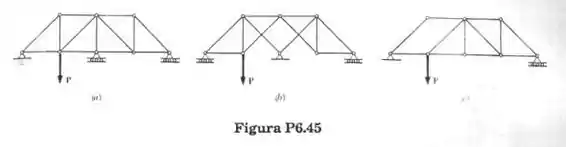
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
- Diagrama de corpo livre da treliça
- Diagrama de corpo livre da treliça
- Diagrama de corpo livre da treliça
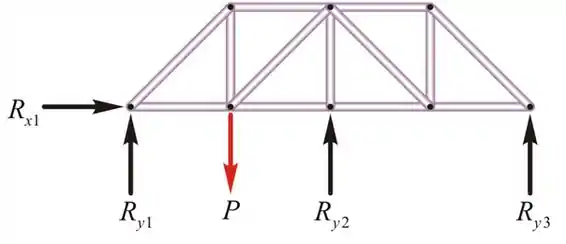
O número de juntas na treliça
Número de membros na treliça,
Número de reações que suportam a treliça,
Um suporte de pino oferece duas reações, enquanto um suporte de rolo oferece apenas uma única reação.
Número de incógnitas na treliça
Número de equações disponíveis
Assim, o número de incógnitas é maior que o número de equações.
Assim, a treliça é completamente restrita e estaticamente indeterminada.
Passo 2
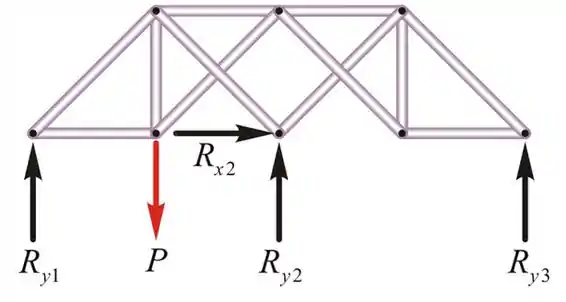
O número de juntas na treliça
Número de membros na treliça,
Número de reações que suportam a treliça,
Um suporte de pino oferece duas reações, enquanto um suporte de rolo oferece apenas uma única reação.
Número de incógnitas na treliça
Número de equações disponíveis
Assim, o número de incógnitas é igual ao número de equações.
Assim, a treliça é completamente restrita e estaticamente determinada.
Passo 3
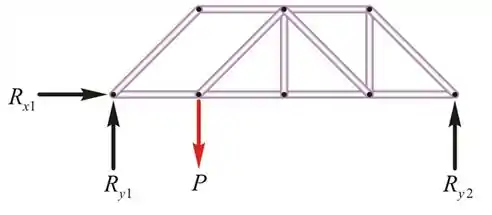
O número de juntas na treliça
Número de membros na treliça,
Número de reações que suportam a treliça,
Um suporte de pino oferece duas reações, enquanto um suporte de rolo oferece apenas uma única reação.
Número de incógnitas na treliça
Número de equações disponíveis
Assim, o número de incógnitas é menor que o número de equações.
Assim, a treliça é parcialmente restrita.
Resposta
Vide o passo a passo.