Classifique cada uma das estruturas dadas como completa parcial ou ineficazmente vinculada. Se completamente vinculada, classifique ainda como determinada ou independente. (Todas as barras podem estar submetidas a tração ou a compressão).
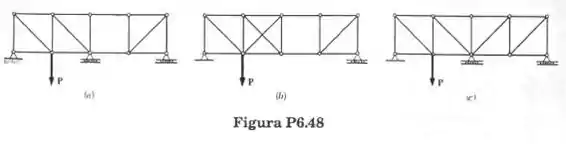
Passo 1
Falaiii meus amores, cêis tão suave?
Bora pra mais uma??
Então, encostaa!!
- Iremos desenhar o diagrama de corpo livre da treliça
- Desenhando o D.C.L da treliça
- Desenhemos o D.C.L da treliça
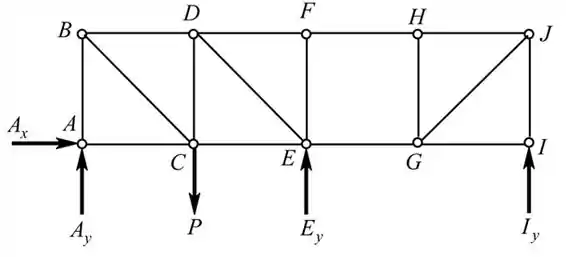
Encontraremos os seguintes parâmetros do carregamento da treliça
Número de barras,
Número de juntas,
Número de reações desconhecidas,
Calcularemos da seguinte maneira
Calcularemos 2 n da seguinte maneira
Uma vez que todas as forças na treliça podem ser determinadas, e A treliça e completamente restrita e determinada.
Passo 2
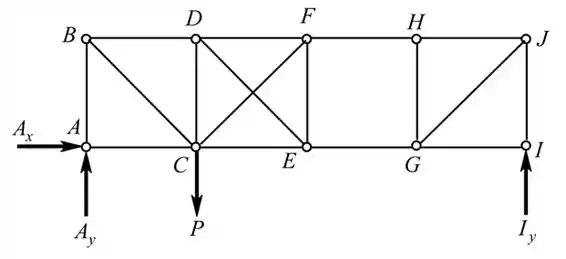
Encontraremos os seguintes parâmetros do carregamento da treliça
Número de barras,
Número de juntas,
Número de reações desconhecidas,
Calcularemos da seguinte maneira
Calcularemos 2 n da seguinte maneira
Uma vez que todas as forças na treliça podem ser determinadas, e A treliça e completamente restrita e determinada.
Considerando o diagrama de corpo livre no nó C
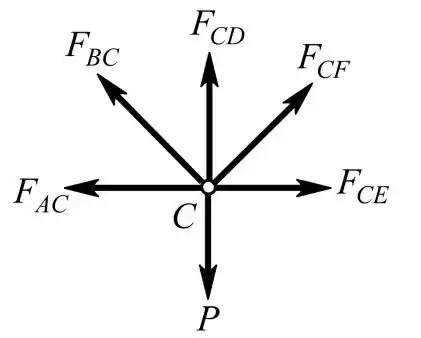
Na junta C, as forças nos membros são desconhecidas e muitas. Sendo assim, as forças em todos os membros não podem ser calculadas.
Mesmo que seja igual a , mas todas as forças na barra não podem ser calculadas. A treliça está incorretamente restringida.
Passo 3
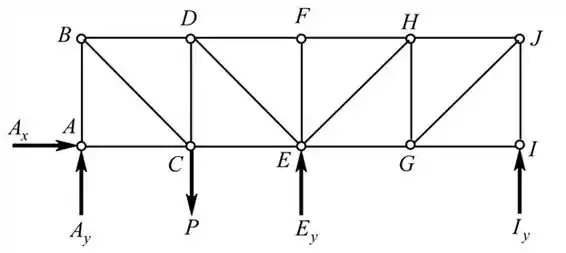
Encontraremos os seguintes parâmetros do carregamento da treliça
Número de barras,
Número de juntas,
Número de reações desconhecidas,
Calcularemos da seguinte maneira
Calcularemos 2 n da seguinte maneira
Uma vez que todas as forças na treliça podem ser determinadas, e A treliça e completamente restrita e indeterminada.
Resposta
Vide o passo a passo.