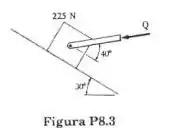
Os coeficientes de atrito entre o bloco de 225 N e o plano inclinado são . Verifique se o bloco está em equilíbrio e calcule o módulo e a direção da força de atrito com .
Passo 1
Alô Alô, galerinha do responde ai, tudo bem?
Bora lá
Vamos considerar o equilíbrio de forças ao longo da direção y
Passo 2
Considerando o equilíbrio de forças ao longo da direção x
O sinal (-) representa a força de atrito assumida na direção oposta
Iremos encontrar a força limite máxima entre o bloco e a superfície
Como a força de atrito de equilíbrio é maior que a força de atrito máxima, o bloco se moverá
Portanto, o bloco se moverá ao longo da superfície.
Passo 3
Agora , iremos encontrar a força de atrito real usando a equação quando o corpo está se movendo
Portanto, a força de atrito necessária do bloco é e a direção da força de atrito é
Resposta
Portanto, o bloco se moverá ao longo da superfície.
Portanto, a força de atrito necessária do bloco é e a direção da força de atrito é