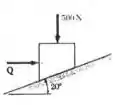
Os coeficientes de atrito entre o bloco e o plano inclinado são . Verifique se o bloco está em equilíbrio e calcule o módulo e a direção da força de atrito com .
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Iremos começar desenhando o nosso D.C.L
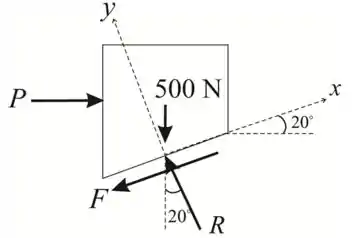
R – representa a reação normal
P – representa a força aplicada
F – representa a força de atrito
Passo 2
Partindo do diagrama e aplicando a condição de equilíbrio:
Considerando algumas das forças ao longo do eixo de y, temos:
Passo 3
Para a força de atrito limite máxima entre o bloco e a superfície é
Considerando as forças ao longo do eixo de x
Passo 4
Ao comparar a força de atrito de equilíbrio e a força de atrito máxima temos . Portanto, a condição de equilíbrio existe.
Logo, a força de atrito é
O sinal (-) representa a força de atrito assumida na direção oposta
Portanto, a força de atrito necessária é .
Resposta
Portanto, a força de atrito necessária é .