O conjunto do painel e os eixos x-y-z anexados giram com uma velocidade angular constante de sobre o eixo z vertical. Simultaneamente, os painéis girar em torno do eixo y como mostrado com uma taxa constante . Determine a aceleração angular do painel A e encontre a aceleração do ponto P para o instante em que .
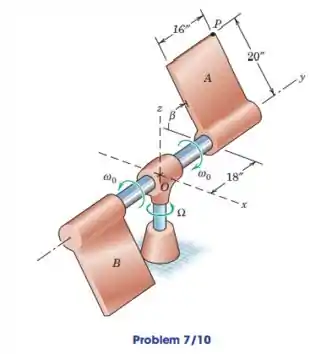
Passo 1
Falaaaai meus amores?
Como estão??
Vem comigo que eu tenho um plano, no caminho eu explicoooo!
Só boraaaaa
Dado que
Velocidade angular constante
Velocidade angular em torno do eixo y,
Aceleração angular do painel A,
Então ,
Passo 2
Aceleração em p,
Onde,