Considere o caso de um pêndulo duplo mostrado na Figura 12.E onde o pêndulo superior possui o comprimento , o comprimento do inferior é de , de maneira similar, as massas da, cabeças são. O movimento acontece somente no plano. Encontre e descreva os modos e coordenadas normais. Assuma pequenas oscilações.
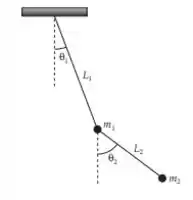
Passo 1
Fala aí galera, beleza? Nessa questão as coordenadas do sistema são dadas na figura:
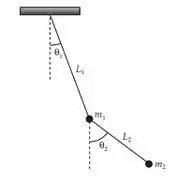
Passo 2
Olha só, daí a energia cinética será:
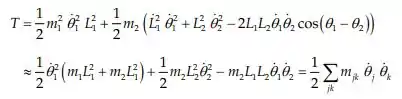
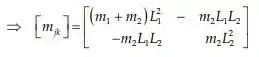
E a energia potencial:
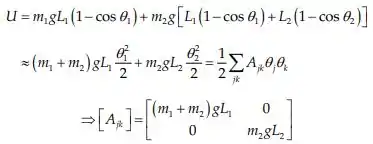
Passo 3
Agora é hora das frequências...
Frequências de oscilação adequadas são soluções da equação:
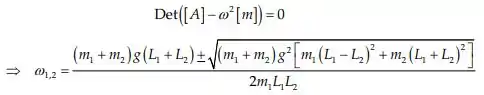
Com isso a autofrequencia para é onde:
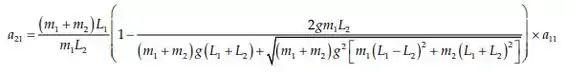
E... a autofrequencia para é onde:
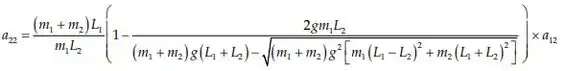
Passo 4
Expressões complicadas no passo anterior né? Mas relaxa que a parada aqui é verificar que têm o mesmo sinal enquanto tem sinais opostos .
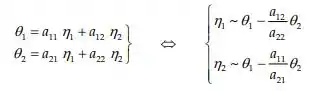
Assim a relação entre as coordenadas e as coordenadas normais é
Daí para visualizar a coordenada normal , vamos deixar . E daí para visualizar a coordenadas normal , vamos deixar que .
Resposta
E olha só que legal, como e , vemos que essas coordenadas normais descrevem dois modos de oscilação. No primeiro, os dois pêndulos se movem em direções opostas e no segundo, os dois pêndulos se movem na mesma direção.