Considere um disco fino composto por duas metades homogêneas conectadas ao longo de um diâmetro do disco. Se uma metade tiver densidade e a outra tiver densidade , determine a expressão da lagrangiana quando o disco rola sem escorregar ao longo de uma superfície horizontal. (A rotação ocorre no plano do disco.)
Passo 1
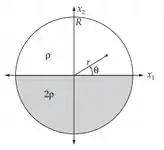
O centro de massa do disco é onde:
Assim o centro de massa pode ser escrito como:
Logo:
Passo 2
O cálculo direto da inércia rotacional em relação a um eixo que passa pelo centro de massa é moroso, então primeiro calculamos em relação ao eixo e então usamos o teorema de Steiner.
Então:
Quando o disco gira sem escorregar, a velocidade do centro de massa pode ser obtida por:
Onde:
Passo 3
A energia cinética pode ser entendida como:
A energia potencial é:
Por fim a Lagrangiana:
Resposta
Ei, a resposta está no passo a passo :)