Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 13.Problemas - Ex. 20

Considere um fio contínuo infinitamente longo com tensão τ . Uma massa M está ligada ao fio em x = 0 Se um trem de onda com velocidade ω k incide da esquerda, mostre que a reflexão e a transmissão ocorrem em x = 0 e que os coeficientes R e T são fornecidos por

R = sin 2 ⁡ θ ,       T = cos 2 ⁡ θ

tan ⁡ θ = M ω 2 2 k τ

Considere cuidadosamente a condição de contorno sobre as derivativas das funções de onda em x = 0 . Quais são as mudanças de fase para as ondas refletidas e transmitidas?

Passo 1

Faaaaaala, galera... Tranquileba??

Fazendo um diagrama do dito no enunciado, temos:

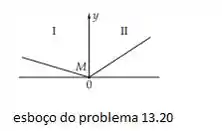
Com a corda dividida em x > 0   e x < 0 . Usando as equações de onda:

Ψ I = A 1 e i ω t - k x + B 1 e i ω t + k x  

Ψ I I = A 2 e i ω t - k x

Com as condições de contorno:

Ψ I x = 0 = Ψ I I x = 0

O que significa que é contínua em x=0. Mas devido a massa M ser juntada em x = 0 , a derivativa da função não vai ser continua nesse ponto. Aa condição naa derivada é obtida ao integrar a função de onda de x = - ϵ até x = + ϵ com limite de ϵ → 0 .

Bora pro próximo passo?!

Passo 2

Obrigado por vir.

Portanto:

M ∂ 2 Ψ ∂ t 2 ​ x = 0 = τ ∂ Ψ I I ∂ x - ∂ Ψ I ∂ x ​ x = 0

Substituindo a equação de onda:

A 1 + B 1 = A 2                                               s i s t e m a   1

i k τ - A 2 + A 1 - B 1 = - ω 2 M A 2

Desse sistema podemos tirar:

A 1 - B 1 = A 2 i k τ - ω 2 M i k τ

De forma que:

A 1 + B 1 A 1 - B 1 = i k τ i k τ - ω 2 M

Assim:

B 1 A 1 = ω 2 M 2 i k τ - ω 2 M = ω 2 M 2 i k τ 1 - ω 2 M 2 i k τ

Passo 3

Definamos:

ω 2 M 2 k τ = P = tan ⁡ θ

Assim:

B 1 A 1 = - i P 1 + i P

Substituindo no sistema 1:

A 2 A 1 = 1 1 + i P

O coeficiente de reflexão R = B 1 A 1 2 como foi dado:

R = B 1 A 1 2 = P 2 1 + P 2 = tan 2 ⁡ θ 1 + tan 2 ⁡ θ = sin 2 ⁡ θ

E o coeficiente de transmissão T = A 2 A 1 2 como foi dado:

T = A 2 A 1 2 = 1 1 + P 2 = 1 1 + tan 2 ⁡ θ = cos 2 ⁡ θ

Assim, aas fases que mudam para as ondas refletidas e transmitidas podem ser dadas diretamente por:

B 1 A 1 = B 1 A 1 e i ϕ B 1 - ϕ A 1 = P 1 + P 2 e i tan - 1 ⁡ 1 P

E:

A 2 A 1 = A 2 A 1   e i ϕ A 2 - ϕ A 1 = 1 1 + P 2   e i tan - 1 ⁡ P

Portanto, desde que as fases mudem, temos:

ϕ B 1 - ϕ A 1 = tan - 1 ⁡ 1 P = tan - 1 ⁡ ( cot ⁡ θ )  

ϕ A 2 - ϕ A 1 = - tan - 1 ⁡ P = - tan - 1 ⁡ ( tan ⁡ θ ) = - θ

Resposta

ϕ B 1 - ϕ A 1 = tan - 1 ⁡ 1 P = tan - 1 ⁡ ( cot ⁡ θ )  

ϕ A 2 - ϕ A 1 = - tan - 1 ⁡ P = - tan - 1 ⁡ ( tan ⁡ θ ) = - θ

E a demonstração segue no passo-a-passo.