Considere um oscilador harmônico relativístico unidimensional para o qual a lagrangiana é
![]()
Obtenha a equação de movimento de Lagrange e mostre que ela pode ser integrada para produzir
![]()
onde a é a amplitude máxima a partir do equilíbrio da partícula oscilante. Mostre que o período
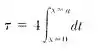
pode ser expresso como
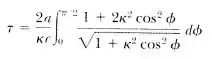
Amplie o integrando em potências de
![]()
e mostre que, para a primeira ordem em k
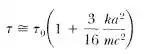
onde é o período não relativístico para pequenas oscilações, .
Passo 1
Fala galera, beleza? Dessa vez vamos começar com a Lagrangiana:
![]()
Daí calculamos:
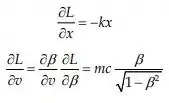
Assim a expressão Lagrangiana do movimento é:
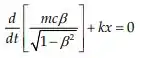
Passo 2
De onde:
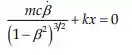
Usando a relação:
![]()
Podemos reescrever as equações acima:
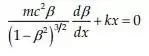
Que pode ser integrada, resultando em:
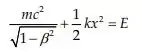
Onde E é a constante de integração.
Passo 3
Pega essa visão, o valor de E é calculado para algum ponto particular no espaço de fase, sendo o mais fácil, acredite em mim, é o mais fácil de verdade rsrsr, :
![]()
Das equações acima temos:
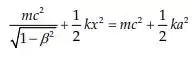
Onde podemos eliminar :
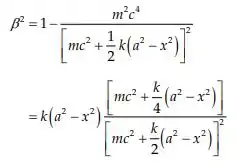
E, portanto:
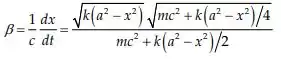
Passo 4
E aí miguxos e miguxas, o período será quatro vezes a integral de de até
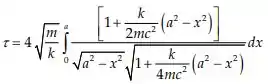
Como x varia entre 0 e a, a variável x/a assume valores no intervalo de 0 a 1 e, portanto, podemos definir
![]()
De onde temos:
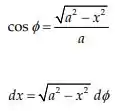
E assim podemos definir o parâmetro adimensional:
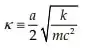
E assim podemos chegar na integral:
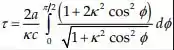
Passo 5
É muito cálculo né? Mas me abandona não, vem comigo, vem... Que já estamos vendo a luz no fim do túnel 😊.
Como para o caso fracamente relativista, podemos expandir o integrando da equação anterior em uma série de potencias de k:
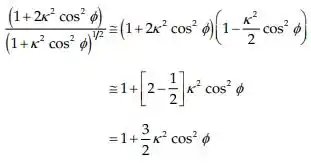
Substituindo:
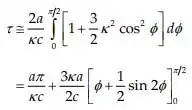
Resposta
Substituindo a expressão de k visto acima, obtemos:
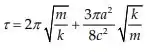
Ou:
![]()