Considere um pêndulo plano simples que consiste de uma massa conectada a um fio de comprimento . Após o pêndulo ser colocado em movimento, o comprimento do fio é encurtado a uma taxa constante
O ponto de suspensão permanece fixo. Compute as funções de Lagrange e Hamilton. Compare a hamiltoniana e a energia total e discuta a conservação de energia para o sistema.
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
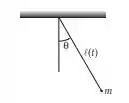
Primeiro precisamos da energia cinética e potencial. A cinética podemos escrever como a parte translacional, que vai depender do comprimento do fio e da parte rotacional, que vai depender do ângulo que o fio está. Segue a figura pra facilitar.
Passo 2
A parte da energia cinética translacional vai ser a parte que depende do comprimento de , ficando
E a parte rotacional, que vai depender de e , ficando
Juntando as duas, a energia cinética total vai ficar
Como o fio está diminuindo, temos que . Substituindo na equação da energia cinética, temos
Para a energia potencial temos
Assim a lagragiana fica na forma
Passo 3
Para a Hamiltoniana precisamos achar o momento conjugado. Já que o único termo que varia é o vamos calcular o momento em relação a ele.
Por essa equação temos que
Escrevendo a Hamiltoniana, temos
Substituindo a forma do momento que achamos acima, ficamos com
Comparando com , temos
Resposta
Como a hamiltoniana é diferente da soma da energia potencial e cinética, a energia não é conservada no sistema.
Mais um problema feito. Bora pra mais um?