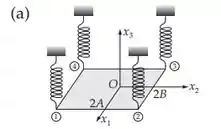
Considere uma placa fina homogênea de massa M que fica no plano com seu centro na origem. Deixe o comprimento da placa em 2A (na direção ) e a largura em 2B (na direção ). A placa é suspensa por um suporte fixo por quatro molas de constante de força iguais k nos quatro cantos da placa. A placa é livre para oscilar, mas com a restrição de que seu centro deve permanecer no eixo . Assim, temos três graus de liberdade: (1) o movimento vertical, com o centro da placa se movendo ao longo do eixo ; (2) um movimento de inclinação perpendicular, com eixo , servindo como um eixo de rotação (escolha um ângulo para descrever o movimento); e (3) um movimento de inclinação lateral, com o eixo servindo como um eixo de rotação (escolha um ângulo para descrever o movimento). Assuma somente pequenas oscilações e mostre que a equaçáo secular possui uma raiz dupla e, consequentemente, o sistema é degenerado. Discuta os modos normais do sistema (Avaliando para modos degenerados, coloque arbitrariamente um dos igual a zero para remover a indefinição). Mostre que a degeneração pode ser removida pela adição à placa de uma barra fina de massa m e comprimento 2A situada (em equilíbrio) ao Iongo dos eixos . Encontre as novas autofrequências do sistema.
Passo 1
A configuração de equilíbrio é mostrada no diagrama (a) abaixo, e as configurações de não equilíbrio são mostradas nos diagramas (b) e (c).
A energia cinética do sistema é:
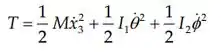
Onde e .
A energia potencial é:
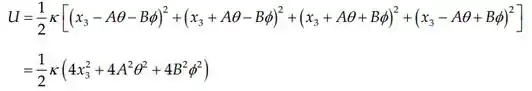
Portanto os tensores e são:

A equação secular será:
![]()
Assim, as frequencias caracteristicas serão:
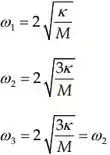
E assim podemos ver que o sistema é degenerativo.
Passo 2
Os componentes do autovetor são encontrados a partir da equação:
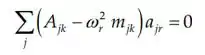
Considerando para remover a indeterminação:
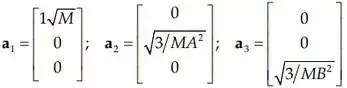
As coordenadas normais serão:
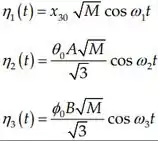
Passo 3
O modo 1 corresponde às oscilações verticais simples da placa (sem inclinação). O modo 2 corresponde a oscilações rotacionais em torno do eixo e o modo 3 corresponde a oscilações rotacionais em torno do eixo .
A degenerescência do sistema pode ser removida se a simetria for quebrada. Por exemplo, se colocarmos uma barra de massa m e comprimento 2A ao longo da placa, então o momento de inércia em torno do eixo é alterado:
![]()
E as novas autofrequencias serão:
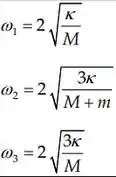
E não haverá mais degeneração.
Resposta
Ei, a resposta está no passo a passo :)