Considere uma placa fina homogênea que repousa no plano . Demonstre que o tensor de inércia assume a forma:
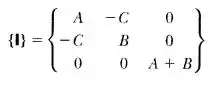
Passo 1
Assume-se que a placa tem espessura desprezível e a massa por unidade de área é . Então os elementos tensores de inércia são:
Definindo e como acima, se torna:
Passo 2
Ainda:
Resposta
Portanto, o tensor de inercia tem a forma: