Considere uma placa plana homogênea de densidade limitada pela espiral logarítmica e raios. Obtenha o tensor de inércia para a origem em r=0 caso a placa esteja no plano. Efetue uma rotaçáo dos eixos de coordenadas para obter os momentos de inércia principais e utilize os resultados do problema anterior para demonstrar que eles são
![]()
Onde
![]()
Passo 1
O limite da placa é dado por . Qualquer ponto possui os componentes:
Os momentos de inercia são:
A integral sobre pode ser definida sobre uma equação trigonométrica característica:
Onde:
Passo 2
De mesmo modo:
Passo 3
Além disso:
Para verificar a integral sobre , nesse caso :
O ângulo através do qual as coordenadas devem ser rotacionadas para fazer diagonal é:
Dessa forma:
E também:
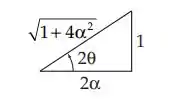
Então:
Usando e , temos:
Passo 4
Dessa forma:
Portanto:
Onde:
De forma similar:
E por fim:
Resposta
Ei, a resposta está no passo a passo :)