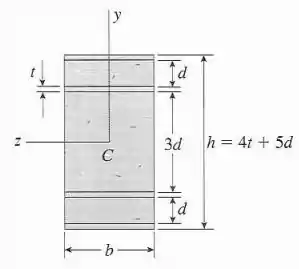
Considere o problema anterior se a viga tem largura , as tiras de alumínio têm espessura , os segmentos de plástico têm alturas e e a altura total da viga é . Os módulos de elasticidade são e , respectivamente. Determine as tensões máximas e no alumínio e no plástico, respectivamente, devido a um momento fletor de .
Passo 1
- Plástico
- Alumínio
Bora lá galera!
Primeiro vamos transformar a seção para um único material, sendo esse o alumínio transformado em plástico.
Com isso, para calcular as tensões máximas no alumínio e no plástico precisamos calcular o momento de inércia de acordo com cada material.
- Plástico
- Alumínio
Logo, o momento de inércia total será:
Passo 2
Agora vamos determinar as tensões máximas no plástico e no alumínio. Logo:
- Plástico
- Alumínio
Equação 6.15
Equação 6.17
Resposta