Considere o problema da partícula se movendo sobre a superfície de um cone, conforme discutido nos Exemplos 7.4 e 8.7. Demonstre que o Potencial efetivo é:

(Observe que, aqui, r é a distância radial em coordenadas cilíndricas, e não coordenadas esféricas; veja a Figura 7.2). Demonstre que os pontos de volta do movimento podem ser obtidos da solução de uma equação cúbica em r. Demonstre também que somente duas das raízes são fisicamente significativas, de modo que o movimento fica confinado entre dois planos horizontais que cortam o cone.

Obrigado por vir.

Substituindo :

Assim, o potencial efetivo é:

No ponto de virada

De forma que:

E seu gráfico é:

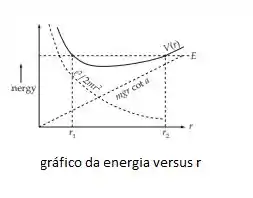
Essa equação tem três raízes, se tentarmos achar as raízes dessas equação graficamente pela interseção e nós constatamos que apenas duas das raízes são reais.