Considere o tensor de inércia a seguir:
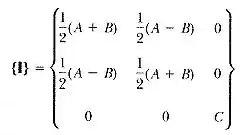
Efetue uma rotação do sistema de coordenadas por um ângulo em torno do eixo . Avalie os elementos do tensor transformado e demonstre que a opção produz a diagonal do tensor de inércia com os elementos A,B e C.
Passo 1
A matriz de rotação é:
O momento do tensor de inercia é transformado de acordo com:
Que pode ser escrito como:
Resolvendo a equação matricial, temos:
Resposta
Se , então: