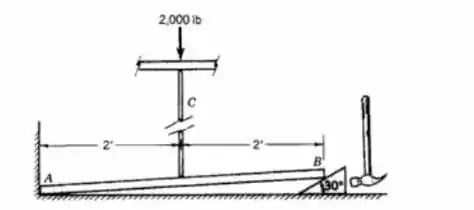
Na construção de edifícios é comum construir um piso ou um telhado sobre suportes temporários que permitem "nivelar" antes de colocar as colunas permanentes no lugar. O esboço abaixo mostra uma das maneiras pelas quais esse "nivelamento" é realizado. A coluna temporária C suporta um peso de 2.000 lb. A inserção da cunha em B levanta uma extremidade da barra rígida AB e, portanto, eleva C pela metade.
(a) Estime a força mínima entre o martelo e a cunha que fará com que a cunha se mova mais para dentro, supondo que todos os coeficientes de atrito sejam 0,3.
(b) O que aconteceria se os coeficientes de atrito fossem muito pequenos? Qual é o valor do coeficiente de atrito que marca a fronteira entre o desempenho desejável e o indesejável?
Passo 1
Assumindo um coeficiente de atrito geral f, quando a cunha está em movimento, a força vegetativa no contato = f × forças normais.
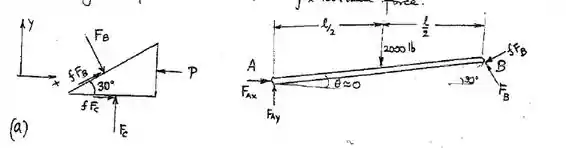
(a)equilíbrio de AB
Equilíbrio da cunha
Isso dá
Para
Passo 2
(b) Se f for muito pequena, a cunha será enviada quando a força P for removida. O border hine ocorre quando a cunha é apenas pré-verificada do transporte para fora pelas forças de atrito. Atravessamos a análise prévia, recolocando em todos os lugares, tornou-se a tendência que estamos nem investigando a sua fuga na direção oposta. Assim obtemos
É requerido ou
Resposta
b.