Consulte a discussão do pião simétrico na seção 11.11. Examine a equação para os pontos de volta do movimento nutacional, ajustando na Equação 11.162. Demostre que a equação resultante é cúbica em e tem duas raízes reais e uma raiz imaginária para .
Passo 1
Considerando temos:
Reorganizando a equação, temos que:
Que é uma equação cúbica.
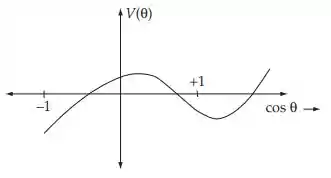
tem a forma mostrada no diagrama. Duas das raízes ocorrem na , e uma raiz está fora desse intervalo e, portanto, é imaginária.
Resposta
Ei, a resposta está no passo a passo :)