Consulte o Exemplo 10.3 relativo à deflexão da linha de prumo de uma partícula em queda no campo gravitacional da Terra. Considere g como sendo definido no nível do solo e utilize o resultado de ordem zero para o tempo de queda, . Efetue um cálculo com aproximação de segundo (isto é, mantenha os termos em ω2) e calcule a deflexão para o sul. Existem três componentes a considerar: (a) Força de Coriolis para a segunda ordem (C1), (b) variação da força centrífuga com altura (C2) e (c) variação da força gravitacional com altura (C3). Demonstre que cada um desses componentes fornece um resultado igual a:

Com C1 = 2/3, C2 = 5/6 e C3 = 5/2. A deflexão total para o sul é, portanto:

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de movimento em um sistema de referência não inercial.

A partir do enunciado temos o esquema do problema:

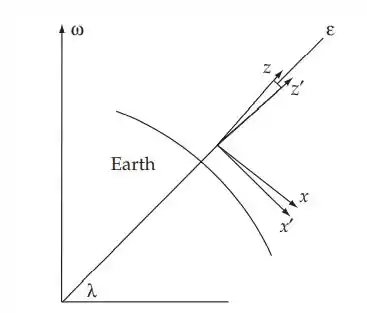
Os pequenos parâmetros que governam as aproximações que precisam ser feitas para encontrar a deflexão ao sul de uma partícula em queda são:

A componente puramente gravitacional é definida da mesma forma que no Problema 10-12. Observe que, embora δ e α sejam pequenos, o produto δα = hω2/g0 ainda é de ordem ω2 e, portanto, espera-se que contribua para a resposta final.

Como a linha de prumo, que define nossa direção vertical, não está na mesma direção da radial externa da Terra, usaremos dois sistemas de coordenadas para facilitar nossa análise. As coordenadas não marcadas para o Hemisfério Norte centrado terão seu eixo x em direção ao sul, seu eixo y em direção a leste e seu eixo z na direção do fio de prumo. As coordenadas com marcação compartilharão sua origem e seu eixo y′ com sua contraparte sem marcação, com os eixos z′ e x′ girados para tornar o eixo z′ um radial externo (veja a figura). A rotação pode ser descrita matematicamente pela transformação:

Onde:

conforme encontrado no Problema 10-12.