Uma corda uniforme de comprimento total pende em equilíbrio sobre um prego liso. Um pequeno impulso faz com que ela se desenrole lentamente do prego. Determine à velocidade da corda no momento em que ela se solta totalmente do prego. Suponha que a corda não pode se elevar ao sair do prego e que esteja em queda livre.
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Nesse exercício temos uma corda pendendo pra um lado de um prego e uma puxada em um lado dela faz com que ela caia. Queremos saber qual a velocidade a corda vai atingir quando se soltar totalmente do prego.
Passo 2
Segue o desenho pra facilitar.
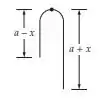
Primeiro vamos analisar a força na corda nesse momento. Temos a força que a parte a direita faz e a força que a esquerda faz. Temos também a densidade da corda que pode ser representada como . Assim, a força que cada parte faz vai ser
E a força da esquerda vai ser
Como uma está indo pra cima e a outra pra baixo, subtraímos as duas forças pra ter a força resultante.
Passo 3
Agora achamos o momento, por
Aplicando a 2ª Lei de Newton, temos
Reescrevendo a derivada da velocidade com o tempo para ficar na forma da derivada da velocidade em relação a posição
Com essa mudança, nossa equação fica
Integrando dos dois lados da equação temos
Como quando temos . Então temos que . Assim nossa equação fica
Como a corda inicialmente estava em equilíbrio, tínhamos inicialmente um comprimento para um lado e para o outro, igualmente. Então a corda precisa percorrer um comprimento para sair do prego. Então, substituímos na nossa equação da velocidade, encontrando
Resposta
A velocidade quando ela sai do prego é de .
Mais um problema feito. Bora pra mais um?