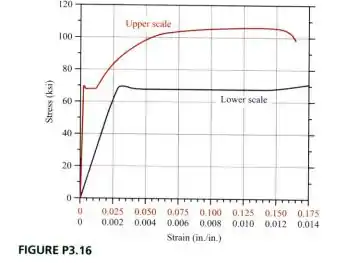
Um corpo de prova de tração de aço 1045 laminado a quente com diâmetro de 0,505 in. e um comprimento padrão de 2,00 in. foi testado para fratura. Os dados de tensão e deformação obtidos durante o teste são mostrados em Figura P3.16. Determinar
(a) o módulo de elasticidade.
(b) o limite proporcional.
(c) a resistência máxima.
(d) a resistência ao escoamento (deslocamento de 0,20%).
(e) a tensão de fratura.
(f) a verdadeira tensão de fratura se o diâmetro final do corpo de prova em a localização da fratura foi de 0,392 in.
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
- Calculando o módulo de elasticidade que pode ser encontrado pela lei de Hooke, temos
- A proporcionalidade da curva de tensão deformação é considerada como 60 ksi
- A resistência máxima é a tensão máxima que o corpo de prova pode suportar. Partindo da curva de tensão deformação considerando a escala superior, podemos encontrar que a tensão máxima até a qual o corpo de prova pode suportar a tensão é de 103 ksi.
- A resistência ao escoamento é definida como a tensão na qual ocorre uma quantidade predeterminada de deformação permanente. A partir da curva tensão – deformação podemos observar que a deformação permanente é encontrada em uma tensão de 68 ksi.
- A tensão de fratura é a tensão normal na área da seção transversal mínima no início da fratura. Partindo da curva de tensão deformação na escala superior, podemos observar que a fratura começa com uma tensão de 97 ksi.
- O diâmetro no local da fratura é de 0.392 in
Portanto, o módulo de elasticidade é de
Passo 2
Escrevendo o limite proporcional da curva da seguinte maneira
Portanto, o limite proporcional é de .
Passo 3
Portanto, a força final é .
Passo 4
Portanto, a força de rendimento é de
Passo 5
Portanto a tensão de fratura é .
Passo 6
Calculando a área da seção transversal do corpo de prova de aço antes da fratura
Calculando a área da seção transversal na fratura
Passo 2
A verdadeira tensão de fratura pode se encontrada utilizando a tensão de fratura obtida da curva de tensão deformação
Calculando a tensão de fratura verdadeira
Portanto, a verdadeira tensão de fratura é .
Resposta
Vide o passo a passo.