Um corpo simétrico se move sem influência de forças ou torques. Considere que o eixo , de simetria do corpo e L estejam ao longo de . O ângulo entre e . Considere e L inicialmente no plano . Qual é a velocidade vetorial angular do eixo de simetria em torno de L em termos de ?
Passo 1
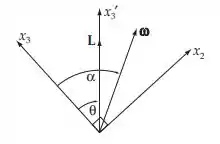
Inicialmente:
Portanto:
Como , temos:
Que se torna:
Da figura inicial podemos construir o triangulo abaixo:
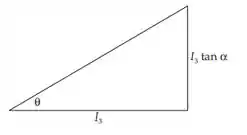
Onde:
Realizando as substituições:
Resposta
Ei, a resposta está no passo a passo :)