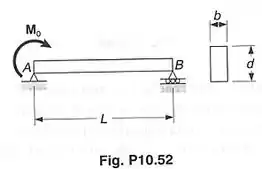
Determinar a energia de deformação da barra prismática , levando em conta os efeitos das tensões normais e das tensões cisalhantes.
Passo 1
E aí, galerinha! Prontos para uma questão de energia de deformação?
Essa questão quer que a gente calcule a energia de deformação total da barra .
Essa energia total é a soma entre a energia causada pelo momento fletor e a energia causada pela força cortante presente na barra.
Nós calculamos através de uma integral (equação 10.17 do livro).
onde é o módulo de elasticidade do material da barra, é o momento de inércia da seção transversal da barra e é o comprimento da barra.
Já a energia é calculada por uma equação sem integral que se encontra abaixo. Essa equação é valida para uma força cortante constante ao longo da barra.
onde é o módulo de elasticidade transversal do material da barra e é a área da seção transversal da barra.
Agora que temos essas equações, nos falta achar quanto vale e para achar . Então vamos calcular primeiro!
Passo 2
Para calcular o momento fletor , precisamos achar quanto vale a força de reação presente no ponto da barra. Para isso, fazemos o equilíbrio de momento no ponto . Escolhemos o ponto , porque nesse ponto a força desconhecida de reação no ponto não tem braço de alavanca e não aparece na equação de equilíbrio da barra.
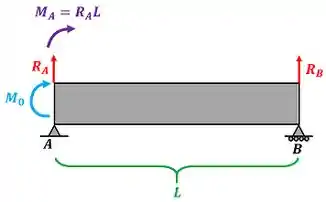
Como o momento da força e o momento fazem a barra girar no sentido horário, colocamos um sinal de menos na frente desses dois momentos na equação de equilíbrio de momentos.
Essa equação de equilíbrio de momentos, diz que a soma dos momentos deve valer zero.
Agora podemos achar quanto vale o momento fletor no próximo passo.
Passo 3
Para achar fazemos um corte imaginário na barra a uma distância do ponto . Com isso, a barra vai ser dividida na parte esquerda e na parte direita. Encontramos , fazendo o equilíbrio de momento da parte esquerda da barra no ponto .
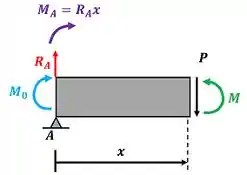
Como podemos ver, o braço de alavanca da força no ponto é zero. Logo, seu momento vale zero. Além disso, lembramos de novo que, como o momento da força e o momento fazem a barra girar no sentido horário, colocamos um sinal de menos na frente desses dois momentos na equação de equilíbrio de momentos.
Passo 4
Como achamos o momento fletor , só falta achar a força cortante para calcular .
Achamos , fazendo o equilíbrio de forças da parte esquerda da barra.
Esse equilíbrio diz que a soma das forças tem que dar zero.
Atenção! Como a força cortante está pra baixo, ele deve gahar um sinal de menos.
Substituindo esse valor de força cortante na equação de , achamos .
Antes, precisamos lembrar que a área é igual a vezes .
Agora sim! Vamos substituir e .
Vamos achar e no próximo passo.
Passo 5
Antes de resolver a integral de , precisamos lembrar que o momento de inércia de uma área retangular vale:
Pronto, substituindo e na integral, achamos !
Tirando as constantes de dentro da integral:
Somando com , achamos .
Shoooow! Enfim achamos a resposta que a questão queria!