Determine a altura na qual uma bola de bilhar deveria bater de modo a rolar sem nenhum escorregamento inicial.
Passo 1
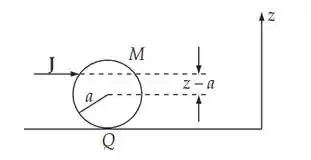
A bola de bilhar recebe um impulso , ou seja, uma força é aplicada durante um curto intervalo de tempo , então:
Passo 2
As equações de movimento são:
Que nesse caso gera:
Passo 3
Como:
Assim após a aplicação do impulso, temos:
Passo 4
Assim:
Onde:
Passo 5
A velocidade em qualquer ponto na bola é dada por:
Para o ponto de contato , isso se torna:
Resposta
Assim para a bola rolar sem escorregar, , e temos:
Então: