Determine o centro de massa de um cone uniformemente sólido com diâmetro da base 2a e altura h.
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
O diagrama (um desenho) do que o enunciado pede facilita a visualização do que é necessário para resolver o problema:
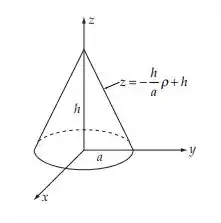
Por simetria, temos que:
Usando coordenadas cilíndricas (), sendo a densidade de massa:
O centro de massa está no eixo, a 3h/4 do vértice do cone.
Resposta
Ver passo a passo.