Determine os eixos e os momentos de inércia principais de um hemisfério uniformemente sólido de raio ô e massa m em torno de seu centro de massa.
Passo 1
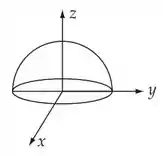
Deixando a superfície do hemisfério sobre o plano conforme a figura. A densidade de massa pode ser determinada por:
Agora vamos calcular o centro de massa do hemisfério, devido a simetria temos:
Utilizando coordenadas esféricas:
Passo 2
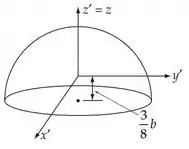
Agora vamos calcular o tensor de inercia com relação aos eixos atravessando o centro de massa do hemisfério:
Por simetria:
Assim vemos que os eixos da figura são os eixos principais, além disso devido a simetria :
Em que é igual ao momento de inercia em relação aos eixos originais:
Assim, temos:
E ainda:
Resposta
Dessa forma os principais eixos são os exibidos na figura do Passo 2, e os momentos de inercia principais são: