Determine as equações dos esforços seccionais das vigas balcão (de raio r e ângulo central ) situadas no plano XY e esquematizadas na próxima figura. A partir dessas equações, trace os correspondentes diagramas para o caso de .
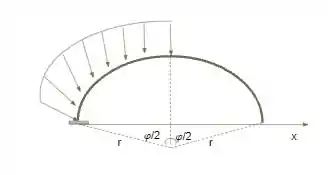 ii)
ii)
Passo 1
E aí.....tudo belezinha?
Considerando o ângulo apresentado, devemos utilizar as equações de equilíbrio apresentadas logo abaixo.
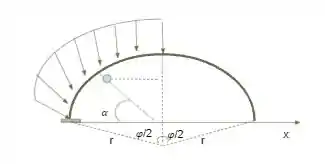 Além das equações de equilíbrio devemos levar em conta as relações que serão retiradas da separação abaixo.
Além das equações de equilíbrio devemos levar em conta as relações que serão retiradas da separação abaixo.
Passo 2
Considerando isso podemos ter novas equações de momentos, sendo mostradas abaixo.
Considerando isso temos
Ao considerarmos , temos:
Passo 3
Considerando isso os gráficos ficarão como demonstrados logo abaixo;

E agora, bora para a próxima questão =)
Resposta
Ei, a resposta está no passo a passo :)